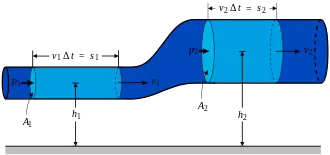
 Luồng khí qua ống Venturi.
Luồng khí qua ống Venturi.
Trong thủy động lực học, nguyên lý Bernoulli giải thích rằng sự tăng vận tốc của chất lưu sẽ đồng thời làm giảm áp suất hoặc thế năng của chất lưu đó.[1][2] Đó chính là nguyên lý Bernoulli, một điều kiện cần thiết trong lĩnh vực cơ học môi trường liên tục, được đặt theo tên của nhà khoa học Daniel Bernoulli từ cuốn sách "Hydrodynamica" năm 1738.[3][2]
Ứng dụng của nguyên lý Bernoulli
Nguyên lý Bernoulli có thể áp dụng cho nhiều loại chất lưu và được biểu diễn dưới dạng phương trình Bernoulli. Phương trình này có các dạng khác nhau tùy thuộc vào loại chất lưu. Đối với dòng chảy không nén được (chẳng hạn như dòng chất lỏng) và cả dòng chảy nén được (chẳng hạn như dòng khí) với vận tốc nhỏ hơn tốc độ âm thanh (số Mach) (thường là nhỏ hơn 0,3), nguyên lý Bernoulli đơn giản có thể được áp dụng. Trong một số trường hợp, nguyên lý Bernoulli cũng có thể áp dụng cho dòng chảy nén được với vận tốc lớn hơn số Mach (xem cách suy luận phương trình Bernoulli).
Cơ chế hoạt động
Nguyên lý Bernoulli là kết quả của định luật bảo toàn năng lượng. Nó khẳng định rằng trong một dòng chảy ổn định, tổng mọi dạng năng lượng trong chất lưu dọc theo đường dòng là như nhau tại mọi điểm trên đường dòng đó. Điều này đòi hỏi tổng động năng, thế năng và nội năng phải là hằng số.[2] Do đó, sự tăng vận tốc của chất lưu - điều đó bao gồm tăng áp suất động và động năng - xảy ra đồng thời với sự giảm (tổng của) áp suất tĩnh, thế năng và nội năng. Khi chất lưu chảy ra khỏi một nguồn, tổng mọi dạng năng lượng sẽ là như nhau trên mọi đường dòng bởi vì trong nguồn, năng lượng trên một đơn vị thể tích (tổng áp suất và thế năng hấp dẫn ρgh) là như nhau ở khắp nơi.[4]
Nguyên lý Bernoulli cũng có thể suy luận trực tiếp từ định luật thứ hai của Newton. Nếu một thể tích nhỏ của chất lưu chảy từ vùng có áp suất cao đến vùng có áp suất thấp, áp suất phía sau của nó sẽ lớn hơn áp suất phía trước. Điều này dẫn đến tổng hợp lực trên đơn vị thể tích, tạo ra gia tốc dọc theo đường dòng.[5][6][7]
Ứng dụng thực tế
Các hạt chất lỏng chỉ chịu áp suất và trọng lượng của chúng. Trong một dòng chất lỏng chảy theo phương ngang và dọc theo tiết diện của đường dòng, vận tốc tăng lên chỉ có thể do chất lỏng chuyển đến từ vùng có áp suất cao hơn sang vùng có áp suất thấp hơn; và nếu vận tốc giảm, chỉ có thể do chất lỏng chuyển đến từ vùng có áp suất thấp hơn sang vùng có áp suất cao hơn. Kết quả là trong dòng chất lỏng chảy theo phương ngang, vận tốc lớn nhất xuất hiện khi áp suất nhỏ nhất, và vận tốc nhỏ nhất xuất hiện khi áp suất cao nhất.[8]
Phương trình dòng không nén được
Trong hầu hết các chất lỏng, và khí có vận tốc nhỏ hơn số Mach, mật độ của một lượng chất lỏng có thể coi là không đổi, bất kể áp suất biến đổi trong chất lỏng. Do đó, chất lưu có thể coi là không nén được và gọi là dòng không nén được. Phương trình Bernoulli ban đầu chỉ đúng cho dòng không nén được. Dạng phương trình Bernoulli phổ biến, đúng tại một điểm bất kỳ dọc theo đường dòng là:
với:
- v là vận tốc của dòng chất lỏng tại điểm trên đường dòng.
- g là gia tốc trọng trường.
- z là cao độ của điểm so với một mặt phẳng tham chiếu.
- p là áp suất tại điểm đó.
- ρ là mật độ tại mọi điểm trong chất lỏng.
Đối với trường lực bảo toàn, phương trình Bernoulli có thể tổng quát thành:
với Ψ là lực thế tại điểm đang xét trên đường dòng. Ví dụ đối với trường hấp dẫn của Trái Đất, Ψ = gz.
Tổng kết
Nguyên lý Bernoulli là một nguyên lý cơ bản trong cơ học môi trường liên tục. Nó giải thích mối quan hệ giữa vận tốc, áp suất và thế năng của chất lưu trong dòng chảy. Sự hiểu biết về nguyên lý Bernoulli không chỉ hữu ích trong lĩnh vực kỹ thuật, mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như hàng không, hàng hải, năng lượng tái tạo, và nhiều hơn nữa.
Tham khảo:
- Đông Anh. (2022). Nguyên lý Bernoulli. XSecret. Truy cập từ đây.